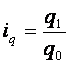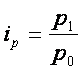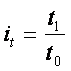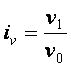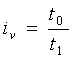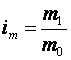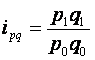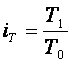ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9.

Расчёт индивидуальных индексов.

Студент должен:

знать:

-   область применения и методику расчёта индивидуальных индексов;

уметь:

-   исчислить индивидуальные индексы количественных и качественных показателей;

-   формулировать вывод по полученным результатам.

Методические указания

Индексы – это относительные величины сравнения сложных статистических совокупностей или их отдельных единиц. Индекс представляет собой относительный показатель, выражающий соотношение величин какого – либо явления во времени, в пространстве, или же сравнение фактических данных с любым эталоном (планом, прогнозом, нормативом и т.д.).

На практике индивидуальные (частные) индексы принято обозначать символом i (начальная буква латинского слова index). Знак внизу справа у индексируемого показателя означает период: 0 –базисный, 1 – отчётный, или же уровень показателя: пл – плановый, ф – фактический, н – нормативный. Помимо этого используются определённые символы для обозначения индексируемых показателей:

Индексируемый показатель	Символ для обозначения индексируемого показателя
Физический объём продукции (товара) в натуральном выражении	q
Цена единицы продукции (товара)	p
Себестоимость единицы продукции	z
Затраты времени на производство единицы продукции	t
Выработка продукции в натуральном выражении на одного рабочего или в единицу времени	v
Удельный расход материала	m
Выработка продукции в стоимостном выражении на одного рабочего или в единицу времени	w
Общие затраты времени на производство продукции (Т=t×q) или численность рабочих (или персонала)	T
Стоимость продукции определённого наименования, или товарооборот	p×q =Q;
Издержки производства продукции определённого наименования	z×q =З

Индивидуальными называются индексы, которые отражают результат сравнения однотоварных явлений, т.е. они характеризуют изменение отдельных элементов сложного явления.

По базе сравнения индивидуальные индексы можно разделить на две группы: динамические и территориальные. Динамические индексы отражают изменение явлений во времени. Например, индекс цен изделий отдельных наименований в 2009 году по сравнению с предыдущим годом; индекс физического объёма производства изделий отдельных наименований в апреле по сравнению с мартом текущего года. Динамические индексы бывают базисные и цепные. Территориальные индексы применяются для межрегиональных сравнений: например, индекс цен на бензин марки АИ 92 в Москве по сравнению с Красноярском.

По объекту исследования индивидуальные индексы можно подразделить на индексы: производительности труда, себестоимости, цен, физического объёма продукции, численности персонала и т.д.

По характеру объекта исследования индивидуальные индексы могут быть индексами количественных (объёмных) показателей и индексами качественных показателей. В основе такого деления  индексов лежит вид индексируемой величины. Например, к количественным индексам относится индекс физического объёма продукции определённого наименования, а к качественным индексам – индекс цен на изделия определённых наименований.

Перечень и формулы расчёта индивидуальных индексов представим в таблице:

Наименование индекса	Формула расчёта	Что показывает индекс
Индивидуальный индекс физического объёма продукции		Во сколько раз возрос (или уменьшился) физический объём продукции в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс цен		Во сколько раз возросла  (или уменьшилась) цена единицы продукции (товара) в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс себестоимости		Во сколько раз возросла (или уменьшилась) себестоимость единицы продукции (товара) в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс трудоёмкости		Во сколько раз возросла (или уменьшилась) трудоёмкость единицы продукции в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс  выработки (производительности труда)		Во сколько раз возросла (или уменьшилась) производительность труда в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс  выработки по трудовым затратам		Во сколько раз возросла (или уменьшилась) производительность труда в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс удельного расхода материала		Во сколько раз возрос (или уменьшился) удельный расход материала в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс стоимости продукции (какого-либо товара)		Во сколько раз возросла (или уменьшилась) стоимость продукции (какого- либо товара) в отчётном периоде по сравнению с базисным периодом
Индивидуальный индекс численности работников		Во сколько раз возросла  (или уменьшилась) численность работников в отчётном периоде по сравнению с базисным периодом

Рассмотрим взаимосвязь  следующих индексов:

Например: пусть имеются значения показателя Х за два периода

Базисный (предыдущий) период	Отчетный (текущий) период
Фактически	По плану	Фактически
Хбаз	Хпл	Хф

Х_баз –фактическое значение показателя в базисном периоде;

Х_пл - значение показателя по плану в отчётном периоде;

Х_ф -  фактическое значение показателя в отчётном периоде.

Индекс планового задания   (1)   =>             

Индекс выполнения плана  (2)    =>             

Индекс динамики                 (3)

Из формулы (1) выразим Х_баз, а из формулы (2) выразим  Х_ф и подставим полученные выражения в формулу (3). Получили формулу (4).

                       (4)

т.е. произведение цепных индексов равно базисному индексу.

Например:

Планом промышленного предприятия предусматривалось увеличить физический объём продукции на 2% по сравнению с базисным периодом.

План выпуска продукции в натуральном исчислении недовыполнен на 0,5%.

Как изменился физический объём выпуска продукции в отчётном периоде по сравнению с базисным периодом?

Решение:

Необходимо исчислить значение индекса динамики:

i_дин.= i_{пл. зад.} × i_{вып. пл. .}

Индекс планового задания

Индекс выполнения плана

Индекс динамики         i_дин.=1,02×0,995=1,015 ,

т е физический объём продукции в отчётном периоде вырос на 1,5% по сравнению с базисным периодом.

При расчёте индексов применяется следующее правило:

Если произведение двух или нескольких показателей представляет собой новый показатель, имеющий реальный экономический смысл, то произведение одноимённых индексов показателей - сомножителей равно индексу нового показателя. Это правило можно представить в таком виде:

Если  a × b = c,                     то                   i_с= i_а × i_b

[Когда речь идёт об одноимённых индексах, то имеются в виду, например, индексы динамики.]

Пример: Как изменилась стоимость продукции «А», если физический объём продукции  уменьшился на 4%, а цена выросла на 2,5% по сравнению с базисным периодом?

Решение:

Стоимость продукции «А» можно представить в виде произведения физического

объёма продукции q на цену одной единицы продукции p          

Аналогичное соотношение можно записать и для индексов динамики этих показателей:                

Индекс динамики физического объёма продукции       

Индекс динамики цены                             

Индекс динамики стоимости продукции        

т.е. стоимость продукции «А» уменьшилась на 1,6% по сравнению с базисным периодом.

Ещё пример: Как изменилась себестоимость единицы продукции в отчётном периоде по сравнению с базисным периодом, если индекс физического объёма продукции составил 1,017, а сумма затрат на производство этой продукции выросла на 4,8%?

Решение:

Себестоимость единицы продукции можно исчислить путём деления общей суммы затрат на производство на физический объём продукции:                   

Аналогичное соотношение можно записать и для индексов динамики этих показателей:        

Индекс динамики суммы затрат на производство  

Индекс динамики физического объёма продукции задан условием i_q =1,017

Индекс динамики себестоимости единицы продукции 

т.е. себестоимости единицы продукции увеличилась на 3% по сравнению с базисным периодом.