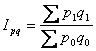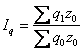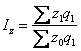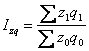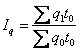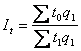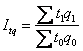ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10.

Расчёт общих индексов.

Студент должен:

знать:

-   область применения и методику расчёта общих индексов;

уметь:

-   исчислить общие индексы количественных и качественных показателей;

-   формулировать вывод по полученным результатам.

Методические указания

Общими индексами называются индексы, выражающие обобщённые результаты изменения всех единиц изучаемой сложной совокупности. Важной особенностью этих индексов является то, что в них соединены разнородные единицы совокупности и такие индексы позволяют изучать влияние отдельных факторов на изменение изучаемого явления. Если индексы охватывают не все элементы сложного явления, а только их часть, то такие индексы называются групповыми индексами, или субиндексами. Групповые      индексы отражают закономерности в развитии отдельных частей изучаемых         явлений. В таких индексах проявляется их связь с методом группировок.

В зависимости от формы построения различают общие индексы агрегатные и средние. Средние индексы, в свою очередь, делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной формой экономических индексов. Средние индексы – производные, они получаются в результате преобразования агрегатных индексов.

По характеру объекта исследования общие индексы подразделяются на индексы количественных (объёмных) показателей и индексы качественных показателей. В основе такого деления  индексов лежит вид индексируемой величины. Например, к количественным индексам относится индекс физического объёма продукции, а к качественным индексам – индекс цен на продукцию.

По составу явления можно выделить две группы сложных индексов: индексы  постоянного (фиксированного) состава и индексы переменного состава. Деление индексов на  эти две группы используется для анализа динамики средних показателей.

С помощью экономических индексов решаются следующие задачи:

-                 измерение динамики социально – экономических явлений за два и более периодов времени;

-                 измерение динамики среднего экономического показателя;

-                 измерение соотношения показателей по различным регионам;

-                 определение степени влияния изменений значений одних показателей на динамику других показателей;

-                 пересчёт значения макроэкономических показателей из фактических цен в сопоставимые.

Каждая из этих задач решается с помощью различных индексов.В экономических расчётах чаще всего используются общие индексы, которые характеризуют изменение совокупности в целом. Построение этих индексов и является содержанием индексной методологии. В индексной теории сложились две концепции: синтетическая и аналитическая. Они по-разному интерпретируют общие индексы.

Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных (разнотоварных) явлений, отдельные части или элементы которых непосредственно несоизмеримы, и поэтому индексы – показатели синтетические. Например, предприятие выпускает несколько видов продукции, имеющей различное назначение и единицы измерения. Следовательно, путём суммирования количества произведённых товаров различных видов нельзя получить показатель физического объёма продукции, Методология построения общих индексов предусматривает, прежде всего, приведение разнотоварных явлений  к соизмеримому виду.

В аналитической теории индексы рассматриваются как показатели, необходимые для измерения влияния изменения составных частей, компонентов, факторов сложного явления на изменение уровня этого явления. Например, изменение общей величины стоимости продукции в отчётном периоде по сравнению с базисным периодом связано как с изменением физического объёма выпущенной продукции, так и с изменением цен по каждому виду продукции. Поэтому индексная методология предусматривает определение влияния каждого из факторов на изменение уровня изучаемого явления.

Таким образом, общие индексы являются и синтетическими и аналитическими показателями.

Общие индексы строят как для количественных, так и для качественных показателей.

В зависимости от цели исследования и наличия исходных данных используют различную форму построения общих индексов: агрегатную или средневзвешенную.

Основной формой общих индексов являются агрегатные индексы. Агрегатный индекс – это сложный относительный показатель, характеризующий среднее изменение социально – экономического явления, состоящего из несоизмеримых элементов.

Своё название агрегатные индексы получили от латинского «aggrego», что значит «присоединяю». В числителе и знаменателе агрегатных индексов содержатся соединённые наборы – агрегаты элементов изучаемой совокупности. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых изменяется (индексируемая величина), а другая остаётся неизменной в числителе и знаменателе (вес индекса).

Для вычисления индекса надо иметь не менее двух величин изучаемого явления. Основным элементом индексного соотношения является индексируемая величина. Под индексируемой величиной понимают признак, изменение значения которого является объектом изучения.

В сложных совокупностях сопоставимость разнородных единиц достигается путём введения специальных сомножителей индексируемых величин. Эти сомножители называются весами – соизмерителями. Их роль при определении агрегатных индексов состоит в том, чтобы обеспечить переход от натуральных измерителей разнородных единиц совокупности к однородным единицам. При этом в числителе и знаменателе агрегатного индекса изменяются лишь значения индексируемой величины, а их веса – соизмерители остаются на одном уровне. Это необходимо для того, чтобы на величине индекса сказывалось лишь влияние изучаемого фактора. Т.о. вес индекса – это величина, служащая для целей соизмерения индексируемых величин.

За каждым экономическим индексом стоят определённые экономические категории. Экономическое содержание индекса определяет методику его расчёта. Методика построения агрегатного индекса предусматривает решение трёх вопросов:

1)              какая величина будет индексируемой;

2)              по какому составу разнородных элементов явления необходимо исчислить индекс;

3)              что будет служить весом при расчёте индекса.

При выборе веса индекса принято руководствоваться правилом: если строится индекс количественного показателя, то веса берутся за базисный период; если строится индекс качественного показателя, то используются веса отчётного периода.

Например, общий индекс количественного показателя – физического объёма продукции имеет вид: 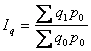, а общий индекс качественного показателя – цены имеет вид:

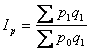
Характеристика общих индексов

Наименование индекса	Формула расчета индекса	Что показывает индекс	Что показывает значение индекса, уменьшенное на 100%, т. е. [I×100-100]	Что показывает разность числителя и знаменателя
Индекс физического объема продукции		Во сколько раз изменилась стоимость продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема	На сколько процентов изменилась стоимость продукции в результате изменения объема ее производства	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) объема ее производства
Индекс цен		Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен	На сколько процентов изменилась стоимость продукции в результате изменения цен	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен
Индекс стоимости продукции (товарооборота)		Во сколько раз возросла (уменьшилась) стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов возросла (уменьшилась) стоимость про дукции в текущем периоде по сравнению с базисным	На сколько рублей увели-чилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции		Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения физического объема ее производства	На сколько процентов изменились издержки производства продукции в результате изме нения объема ее производства	На сколько рублей изменились издержки производства продукции в результате роста (уменьшения) объема ее производства
Индекс себестоимости продукции		Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения ее себестоимости	На сколько процентов изменились издержки производства продукции в результате изме нения ее себестоимости	На сколько рублей изменились издержки произ водства в результате роста (уменьшения) себестоимости продукции
Индекс издержек производства		Во сколько раз возросли (уменьшились) издержки производства продукции, или сколько процентов составил рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным	На сколько процентов возросли (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным	На сколько рублей увеличились (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции		Во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства,        или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменений физического объема ее производства	На сколько процентов изменились затраты времени на производство продукции в результате изме нения объема ее производства	На сколько человеко – часов увеличились (уменьшились) затраты времени на производство продукции в результате роста (уменьшения) объема ее производства
Индекс производительности труда по трудовым затратам		Во сколько раз увеличилась (уменьшилась) производительность труда, или сколько процентов составило снижение (рост) производительности труда в текущем периоде по сравнению с базисным	На сколько процентов изменилась производительность труда в текущем периоде по сравнению с базисным	Абсолютный размер экономии (перерасхода) затрат живого труда в связи с ростом (уменьшением) его производитель ности
Индекс затрат времени на производство продукции		Во сколько раз изменились затраты времени на производство продукции, или сколько процентов составил рост (снижение) затрат времени на производство продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным	На сколько человеко – часов увеличились (уменьшились) затраты времени на производство продукции в текущем периоде по сравнению с базисным

Средняя форма общего индекса.

Агрегатная форма общих индексов является основной формой экономических индексов, а средние индексы – производные, они получаются в результате преобразования агрегатных индексов.

Расчёт средних общих индексов рассмотрим на следующих примерах:

Пример 1. На основании следующих данных определить общее изменение

физического объема выпущенной продукции:

Вид продукции	Стоимость продукции базисного периода, тыс. рублей ()	Изменение количества продаваемых товаров в отчетном периоде по сравнению с базисным периодом, %
А Б В	3800 4400 2100	-10 +12 -22

Указать вид применяемого индекса. Сделать вывод.

Решение:

Общий индекс физического объёма продукции имеет вид: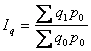 (1)

где  - стоимость продукции отчётного периода в ценах базисного периода, тыс.руб.;

 - стоимость продукции базисного  периода в ценах базисного периода, тыс.руб.

Индивидуальный индекс физического объёма продукции имеет вид:

 (2),        следовательно        (3). Подставим формулу (3) в формулу (1) и получим 

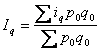     средний арифметический индекс физического объёма продукции

Индивидуальный индекс физического объёма продукции составляет:

Для товара А        

Для товара Б        

Для товара В        

Средний арифметический индекс физического объёма продукции составляет

т.е. в результате [0,970×100-100=-3]  уменьшения физического объёма выпуска продукции в среднем на 3% , стоимость выпущенной продукции в отчётном периоде [9986-10300=-314] уменьшилась по сравнению

с базисным периодом на 314 тыс. руб.

Пример 2. На основании  данных таблицы  вычислить общее изменение

цен на продукцию в отчётном периоде по сравнению с базисным периодом:

Товар	Стоимость продукции отчетного периода в действующих ценах, тыс.руб. ()	Изменение цен  в отчетном периоде по сравнению с  базисным, %
А Б В Г	1060 800 1300 700	-  2 + 15 - 4 + 20

Указать вид применяемого индекса. Сделать вывод

Решение:

Общий индекс цен имеет вид: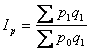 (1)

где  - стоимость продукции отчётного периода в действующих ценах, тыс.руб.;

 - стоимость продукции отчётного периода в ценах базисного периода, тыс.руб.

Индивидуальный индекс цены имеет вид: (2),

следовательно (3).Подставим формулу (3) в формулу (1) и получим

                средний гармонический индекс цен

Индивидуальный индекс цены продукции составляет:

Для товара А        

Для товара Б        

Для товара В        

Для товара Г        

Средний гармонический индекс цен составляет

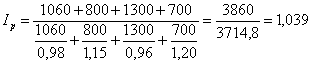
т.е. в результате [1,039×100-100=3,9]  прироста физического объёма выпуска продукции на 3,9% , стоимость выпущенной продукции в отчётном периоде [3860-3714,8=145,2]  увеличилась по сравнению с базисным периодом на 145,2 тыс.руб.

Индексы структурных сдвигов.

При изучении динамики качественных показателей приходиться определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов - изменением значения индексируемого показателя у отдельных групп единиц и изменением структуры явления. Под изменением структуры явления понимается изменение отдельной групп единиц совокупности в общей их численности. Так, средняя заработная плата на предприятии может вырасти в результате роста оплаты труда работников или увеличения доли высокооплачиваемых сотрудников. Снижение трудоёмкости производства единицы продукции по совокупности предприятий отрасли может быть обусловлено повышением производительности труда на предприятиях или концентрацией производства продукции на заводах с низкой трудоёмкостью. Так как на изменение среднего значения показателя оказывают воздействие два фактора, возникает задача определить степень влияния каждого из факторов на общую динамику средней.

Эта задача решается с помощью индексного метода, т.е. путём построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле.

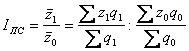
Где I_ПС- индекс переменного состава. Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов)

Индекс постоянного (фиксированного) состава - это индекс, исчисленный с весами, зафиксированными на уровне одного какого- либо периода, и показывающий изменения только индексируемой величины. Индекс фиксированного состава определяется как агрегатный    индекс. Так, индекс фиксированного состава себестоимости продукции рассчитывается по формуле.

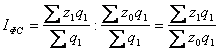
Где I_ФС- индекс фиксированного состава.

Под индексом структурных сдвигов понимают индекс , характеризующий влияния изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле ( при изучении изменения среднего уровня себестоимости )

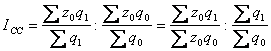
Где Iсс- индекс структурных сдвигов.

Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:     , т.е. индекс переменного состава можно представить в виде произведения индекса фиксированного состава и индекса структурных сдвигов.