ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ № 1.
Группировка статистических данных и
построение рядов распределения.
Студент должен:
знать:
- принципы построения и виды
статистических группировок и статистических рядов распределения;
уметь:
- построить группировку данных в соответствии
с поставленными целями и задачами;
- построить ряд распределения и
представить его графическое изображение;
- произвести перегруппировку
статистических данных для обеспечения их сопоставимости;
- формулировать вывод по полученным
результатам.
Методические указания
Группировка
– это разбиение совокупности на группы, однородные по какому-либо признаку. С
точки зрения отдельных единиц совокупности группировка – это объединение
отдельных единиц совокупности в группы, однородные по каким-либо признакам.
Метод группировки
основывается на следующих категориях – это группировочный
признак, число групп и интервал группировки.
Признак, по которому
осуществляется группировка, называется основанием группировки, или группировочным признаком. Группировочные
признаки могут быть атрибутивными и количественными.
Атрибутивные признаки регистрируются
в виде текстовой записи (например, профессии рабочих, социальная группа
населения). Количественные признаки имеют непосредственное числовое выражение
(стаж работы, размер дохода). Группировка может выполняться по одному признаку
(простая группировка) и по нескольким
признакам (комбинированная группировка).
После определения
основания группировки следует решить вопрос о количестве групп, на которое надо разбить исследуемую совокупность.
При группировке по атрибутивному признаку число групп определяется
количеством соответствующих наименований, т.е.
градаций, видов, состояний у признака, если число этих наименований не
очень велико. Если признак имеет большое количество разновидностей, то
разрабатывается классификация – систематизированное распределение явлений и
объектов на определённые группы, классы, разряды на основании их сходства и
различия.
При группировке по количественному признаку число групп определяется в
зависимости от характера изменения признака и задач исследования. Если
количественный признак меняется прерывно
(дискретно), т.е. может принимать только некоторые – чаще целые значения
(например, тарифный разряд рабочих), то число групп должно соответствовать
количеству значений признака. При небольшом объёме совокупности не следует
образовывать большое число групп, т.к. они будут малочисленными, а показатели, рассчитанные для таких групп не позволят
получить адекватную характеристику исследуемого явления. В каждом конкретном
случае при определении числа групп следует исходить не только из степени колеблемости признака, но ещё учитывать и особенности объекта и цель
исследования.
При непрерывном изменении признак принимает, любые значения (например, стаж работы,
возраст рабочих), поэтому группы ограничиваются значениями признака в интервале
«от и до». На практике используют три вида интервалов: равные, неравные
(постепенно увеличивающиеся) и
специализированные.
Здесь необходимо
учитывать несколько условий:
а) число групп детерминируется
уровнем колеблемости группировочного
признака. Чем значительнее вариация признака, тем больше при прочих равных
условиях должно быть групп;
б) число групп должно отражать
реальную структуру изучаемой совокупности;
в) не допускается выделение пустых
групп. Если проблема пустых групп все же возникает, при проведении структурных
группировок используют неравные интервалы.
Наличие пустых групп или малое число статистических единиц в них свидетельствуют
о неправильном определении их числа.
Группировка с равными
интервалами
строится, если вариация признака проявляется в узких границах и распределение
носит равномерный характер. Величина равного интервала определяется по формуле:
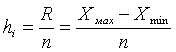(1)
где R – размах вариации определяется как разность между
наибольшим и наименьшим значением признака в совокупности R=Xmax - Xmin;
n – число
групп.
Для расчёта величины
интервала по этой формуле необходимо заранее установить число групп п (при числе наблюдений более 200
используют 10 – 15 групп). Возможен и другой способ установления числа групп. В
этом случае используется формула Стерджесса:
n =1 + 3.322 lgN (2)
где
n – число групп;
N – число
единиц совокупности.
Применение этой формулы
целесообразно при большом числе единиц совокупности. При объёме совокупности
20-25 единиц число групп рекомендуется принимать п ≤ 4.
Формула Стерджесса позволяет определить величину интервала без
предварительного установления числа групп:
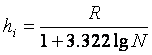(3)
В практических расчетах можно
использовать следующие соотношения, полученные на основании формулы Стерджесса:
|
N |
15-24 |
25-44 |
45-89 |
90-179 |
180-359 |
360 и более |
|
n |
5 |
6 |
7 |
8 |
9 |
10 |
Зависимость
Стерджесса дает хорошие результаты, если совокупность
состоит из большого числа единиц, распределение близко к нормальному,
и при этом используются равные интервалы. Существует еще один способопределения
количества выделяемых групп, он связан с применением
среднеквадратичного отклонения равными и
неравными σ: если величина
(ширина) интервала равна 0,5σ , то выделяется
12 групп, если 2/3σ ,- то 9
групп, если σ – то 6 групп.
Прежде чем определять
размах вариации, из совокупности следует исключить аномальные значения
признака. Если максимальное или минимальное значение сильно отличается от
смежных с ним значений, то для определения величины интервала используют не
максимальное и минимальное значения, а значения, несколько превышающее минимум
и несколько меньше максимума. Полученную по формуле (1) величину округляют. Она является шагом интервала.
Существуют следующие правила
определения шага интервала.
Если величина интервала –
величина, имеющая один знак до запятой (например, 0,66; 1,375; 5,82), то
полученные значения следует округлить до десятых и использовать в качестве шага
интервала (соответственно 0,7; 1,4; 5,8). Когда рассчитанная величина интервала
имеет две значащие цифры до запятой и несколько знаков после запятой, то это
значение надо округлить до целого числа. Пусть величина интервала, исчисленная
по формуле (1.1), равна 12,785. Тогда это значение следует округлить до целого
числа, т.е. до 13. В случае, когда рассчитанная величина интервала представляет
собой трёхзначное, четырёхзначное и так далее число, эту величину необходимо
округлить до ближайшего числа, кратного 100 или 50. Например, 248 следует
округлить до 250. Чаще всего, полученное значение величины (ширины) интервала округляется в бóльшую сторону.
При округлении в меньшую сторону последний интервал делают открытым.
В каждой выделенной группе
рассчитываются следующие параметры:
- верхняя граница интервала;
- нижняя граница
интервала;
- ширина
интервала;
- середина i-го интервала.
Нижней
границей интервала (
) называется
наименьшее
значение признака в интервале - данной группе. Верхней границей интервала (
) называется
наибольшее
значение признака в интервале - данной группе.
Интервалы
группировки бывают равными
и неравными (прогрессивно
возрастающими, прогрессивно убывающими, произвольными, специализированными). Если
вариация признака проявляется в сравнительно узких границах, и распределение
статистических единиц носит достаточно равномерный характер, то строят группировку с
равными интервалами.
На основе рассчитанной ширины интервала
последовательно определяются границы интервалов и . Определение
границ начинается с первой группы. Ее нижняя граница принимается равной минимальному
значению признака в совокупности , т. е. 
, а верхняя
граница определяется как 
Для второй группы нижняя граница
принимается равной верхней границе первой группы, т. е. 
, верхняя
определяется как 
и т. д. В целом границы интервалов
определяются формулами:
и 
Середина интервала
(центральная варианта) 
определяется как
полусумма
верхней и нижней границ, т.е. по
формуле:
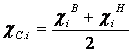
Параметр середина интервала используется при расчете обобщающих
характеристик изучаемой совокупности.
Интервалы могут быть открытыми и закрытыми. Открытые интервалы – это те интервалы, у
которых указана только одна граница: верхняя – у первого, нижняя – у последнего.
Закрытые
интервалы – это те интервалы, у которых обозначены обе границы.
Величина открытого интервала принимается равной величине смежного с ним закрытого
интервала.
Основной задачей распределения
единиц совокупности по группам является
подсчет числа единиц, попавших в каждую из выделенных групп 
. При распределении
единиц наблюдения по выделенным группам, особенно если группировочный
признак является непрерывным, имеет место неопределенность: к какой группе
относить единицы со значениями признака, совпадающими с границами интервалов?
Для устранения неопределенности используют принцип единообразия – такие единицы включаются в группу, в
которой нижняя граница совпадает со значением признака. Например, имеются группы
предприятий по объему производства, млн. руб.: 400
– 450; 450 – 500; 500 – 550; 550 – 600.
К какой группе следует отнести
предприятия с объемом производства 500млн. руб.? В соответствии с принципом
единообразия - ко второй группе. (Т.е нижняя граница – включительно, а верхняя
– исключительно)
Группировка с неравными
интервалами применяются
в статистике, когда значения признака варьируют неравномерно и в значительных
размерах. Неравные интервалы часто применяются в аналитических группировках. В
этом случае интервалы выбираются так, чтобы число единиц в образовавшихся
группах было достаточно велико, т.е. группы были одинаково заполнены.
В типологических
группировках используются специализированные интервалы.
Границы в них устанавливаются там, где начинается переход от одного качества к
другому. Наметить точки перехода можно только на основе теоретического анализа,
используя для выделения типов совокупность признаков, характеризующих различные
стороны изучаемого явления.
Иногда имеющуюся
группировку необходимо несколько изменить: объединить ранее выделенные
относительно мелкие группы в небольшое число более крупных, типичных групп или
изменить границы прежних групп с тем, чтобы сделать группировку сопоставимой с
другими. Такая переработка результатов первичной группировки называется перегруппировкой,
или
вторичной группировкой.
Для
количественной характеристики каждой группы часто выполняют расчет структурных
характеристик. Расчет заключается в определении для каждой группы удельного веса (доли) ее единиц в общем объеме
статистической совокупности. Как и любая относительная величина,
этот показатель может быть определен
в виде коэффициентов, или в виде процентов:
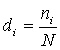или 
Рассчитав такие доли для всех групп, мы
получаем структуру изучаемой статистической совокупности, равную полному набору
долей:
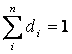или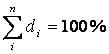 
На основе анализа
показателей структуры делаются соответствующие выводы. В выводах отражаются два
положения:
Какие значения признака
встречаются в совокупности наиболее часто, какие наиболее редко.
Каков характер изменения структуры
явления в зависимости от изменения значения признака. Выводы должны быть сделаны обязательно, иначе пропадает смысл построения группировки.
Метод
группировки предусматривает построение рядов распределения. Статистический ряд
распределения – это упорядоченное распределение единиц совокупности на
группы по определённому варьирующему признаку. В зависимости от признака,
положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения,
построенные по качественным признакам. Такие ряды принято оформлять в виде
таблиц. Атрибутивные ряды распределения характеризуют состав совокупности по
тем или иным существенным признакам. Взятые за несколько периодов времени, эти
данные позволяют исследовать изменение структуры.
Вариационными называют ряды распределения,
построенные по количественному признаку. Любой вариационный ряд состоит из двух
элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариационном
ряду, т.е. варианта – это конкретное значение варьирующего признака. Частоты – это численности отдельных
вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие,
как часто встречаются те или иные варианты в ряду распределения. Сумма всех
частот определяет численность всей совокупности, её объём. Частостями называются частоты, выраженные в долях единицы или в процентах к
итогу. Соответственно сумма частостей равна 1 или
100%.
На практике для анализа рядов
распределения используют их графическое
изображение, позволяющее судить и о
форме распределения, и о характере изменения частот вариационного ряда.
Полигон используется
при изображении дискретных вариационных рядов. Для его построения в
прямоугольной системе координат по оси абсцисс в одинаковом масштабе
откладываются ранжированные значения варьирующего признака, а по оси ординат
наносится шкала для выражения величины частот. Полученные на пересечении
абсцисс и ординат точки соединяют прямыми линиями и получают ломаную линию,
называемую полигоном частот. Иногда
для замыкания полигона крайние точки (слева и справа на ломаной линии)
соединяют с точками на оси абсцисс, в этом случае получается многоугольник. На
оси ординат могут наноситься не только значения частот, но и частостей вариационного ряда.
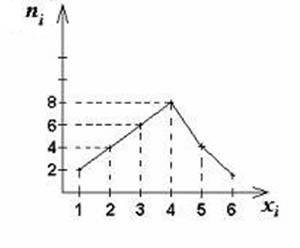
Рис. 1.
Полигон распределения
Гистограмма
применяется для изображения интервального вариационного ряда. При построении
гистограммы на оси абсцисс откладываются величины интервалов, а частоты
изображаются прямоугольниками, построенными на соответствующих интервалах.
Высота столбиков в случае равных интервалов должна быть пропорциональна
частотам. В результате получается гистограмма – график, на котором ряд
распределения изображён в виде смежных друг с другом столбиков. При построении
гистограммы распределения вариационного ряда с неравными интервалами по оси
ординат наносят не частоты, а плотность распределения признака в
соответствующих интервалах. Это необходимо сделать для устранения влияния
величины интервала на распределение и иметь возможность сравнивать частоты. Плотность распределения – это частота,
рассчитанная на единицу ширины интервала, т.е. сколько единиц в каждой группе
приходится на единицу величины интервала.
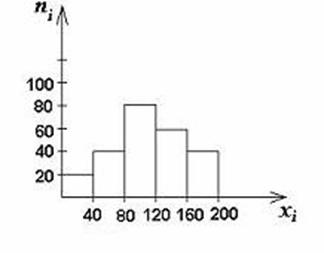
Рис.2. Гистограмма
распределения равноинтервального ряда
Для
графического изображения вариационных рядов может быть использована
кумулятивная кривая. При помощи кумуляты (кривой
сумм) изображается ряд накопленных частот. Накопленные частоты определяются
путём последовательного суммирования частот по группам и показывают, сколько
единиц совокупности имеют значения признака не больше, чем рассматриваемое
значение. При построении кумуляты интервального
вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат
накопленные частоты, которые наносят на поле в виде перпендикуляров к оси
абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и
получают ломаную линию, т.е.
кумуляту. Изображение вариационного ряда в
виде кумуляты особенно эффективно для рядов, частоты
которых выражены в процентах к сумме частот ряда, или же выражены частостями.
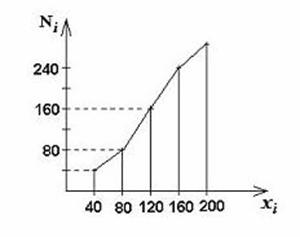
Рис. 3. Кумулята
распределения
Если
при графическом изображении вариационного ряда в виде кумуляты
оси поменять местами, то получим огиву.
С помощью кумулятивных кривых графически изображают процесс концентрации.
Ряд распределения представляет
собой простейшую группировку, в которой каждая выделяемая группа
характеризуется одним показателем – численностью единиц объекта, попавших в
каждую группу. Построение рядов распределения является составной частью сводной
обработки данных, при которой каждая группа единиц характеризуется многими
показателями. Перечень таких показателей формируется в соответствии с целями
статистического исследования и задачами группировки. Для получения обобщённой
характеристики явления следует использовать систему
показателей, которая предусматривает исчисление абсолютных, относительных и средних
величин.
