ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3.

Расчёт степенных средних величин.

Студент должен:

знать:

-     область применения и методику расчёта степенных средних величин;

уметь:

-     исчислять степенные средние величины;

-     формулировать вывод по полученным результатам.

Методические указания

Средней величиной называется обобщающая величина статистической совокупности, выражающая типический уровень изучаемого признака. Она выражает величину признака, отнесённую к единице совокупности.

К степенным средним относятся средняя арифметическая, средняя гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая, средняя кубическая.

Средняя величина всегда обобщает количественную вариацию признака, т. е. в средних величинах погашаются индивидуальные различия признака у отдельных единиц совокупности, обусловленные случайными обстоятельствами. Средняя величина позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям.

Принципы применения средних величин:

1)                Необходим обоснованный выбор признака у единиц совокупности, для которого рассчитывается средняя.

2)                При определении средней величины в каждом конкретном случае следует исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков и особенность имеющихся исходных данных;

3)                Средняя величина должна, прежде всего, рассчитываться по однородной совокупности. Однородную совокупность позволяет получить метод группировки.

4)                Общие средние должны подкрепляться групповыми средними.

5)                Средняя величина не может быть меньше минимального значения и больше максимального значения признака в совокупности.

Область применения и методика расчёта степенных средних величин:

1. Средняя арифметическая

1.1 Средняя арифметическая простая.

При небольшом объёме исходной информации, когда исходные данные не сгруппированы, применяется средняя арифметическая простая,которая рассчитывается по формуле:

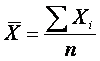
где    ΣX_i - сумма значений;

n- число значений.

Например: В бригаде четверо рабочих в возрасте  21, 22, 23 и 24 года. Средний возраст рабочего бригады составляет

1.2 Средняя арифметическая взвешенная.

Когда исходные данные сгруппированы, то расчёт средней производится по

формуле средней арифметической взвешенной:

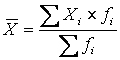
где f_i – частота ряда распределения, с которой отдельные варианты встречаются в совокупности (или удельный вес отдельных значений во всей совокупности).

Например: Рабочие бригады по возрасту распределились следующим образом:

Возраст рабочих, лет (X)	21	22	23	24
Численность рабочих, чел. (fi)	2	3	4	1

Средний возраст рабочего бригады составляет

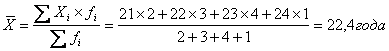
Если исходная информация представлена в виде интервального ряда распределения, то средняя арифметическая взвешенная определяется по формуле:

 

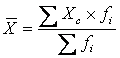
где X_c - центральное (серединное) значение признака в интервале.

Например: По имеющимся данным определить средний стаж рабочего бригады:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
Численность рабочих, чел. (fi)	3	4	7	10	6

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. Среднее значение интервала находится как полусумма нижней границы данного интервала и нижней границы следующего интервала:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
(Xc )

Оформим исходные данные а следующем виде:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
(Xc )	1	3	5	7	9
Численность рабочих, чел. (fi)	3	4	7	10	6

 

Средний стаж рабочего бригады составляет

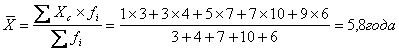
Если в интервальном ряду распределения имеются «открытые» интервалы, то для установления центральных (серединных) значений «открытых» интервалов на каждый из них условно распространяется величина смежного «закрытого» интервала.

Например: Работники организации по величине заработной платы за январь 2010 года распределились следующим образом:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (fi)
До 9	10
9 - 12	24
12 - 15	40
15 - 20	20
20 и выше	6
Итого:	100

Определить по имеющимся данным среднюю зарплату работников организации.

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. На каждый открытый интервал условно распространим величину смежного закрытого интервала:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (fi)	Центральное (серединное) значение интервала (Xc), руб
До 9	10
9 - 12	24
12 - 15	40
15 - 20	20
20 и выше	6
Итого:	100

Частоты при расчете средних арифметических могут быть выражены не только абсолютными величинами, но и относительными величинами – частостями Результаты применительно к одинаковым вариантам будут совпадать. В данном примере численность работников выражена не частотами, а частостями – удельными весами численности отдельных групп во всей совокупности, что не влияет на порядок расчёта средней.

Средняя зарплата работников организации составляет:

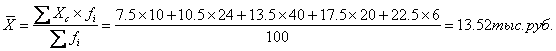
Необходимо небольшое пояснение применительно к расчету средней в интервальных рядах распределения. В действительности распределение отдельных вариантов в пределах интервала может оказаться неравномерным. В этом случае середина интервала будет в той или иной степени отличаться от фактической средней по интервалу. Это в свою очередь может повлиять на правильность общей средней, исчисленной по данным интервального ряда. Степень расхождения зависит от ряда причин. Во-первых, от числа вариант, чем больше число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Во-вторых, от величины интервала. Если интервал невелик, то ошибка будет незначительной, т.к. групповая средняя будет мало отличаться от середины интервала. В-третьих, от характера распределения. Чем симметричнее распределение, тем ошибка меньше. В-четвертых, размер ошибки зависит от принципа построения интервального ряда. При равных интервалах середина интервала будет ближе к средней по данной группе. При наличии открытых интервалов расхождение, как правило, взрастает из-за условного обозначения неизвестных границ. Общая средняя равна средней из частных (групповых) средних, взвешенных по численности соответствующих частей совокупности. Это правило имеет большое значение для всей статистики – организации сбора и обработки данных, их анализа.

Свойства средней арифметической:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты. Другими словами, постоянный множитель может быть вынесен за знак средней.

2. Если от каждой варианты отнять (прибавить) какое-либо произвольное число, то новая средняя уменьшится (увеличится) на то же число:

3. Если каждую варианту умножить (разделить) на какое-то произвольное число, то средняя арифметическая увеличится (уменьшится) во столько раз

4. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится. Дело в том, что веса при исчислении средней арифметической выполняют роль удельного веса (соотношений между группами по количеству единиц). Поэтому замена частот частостями не меняет значения средней.

5. Сумма отклонений отдельных вариантов от средней арифметической всегда равняется нулю.

Перечисленные свойства могут быть использованы для того, чтобы облегчить технику исчисления средней арифметической.

Например. Можно из всех значений признака вычесть произвольную постоянную величину (лучше значение серединной варианты или варианты с наибольшей частотой), полученные разности сократить на общий множитель (лучше на величину интервала), а частоты выразить частостями (в процентах) и исчисленную среднюю умножить на общий множитель и прибавить произвольную постоянную величину. Иногда этот способ расчета средней арифметической также называется способом расчета от условного нуля. Широкое применение для обработки статистических материалов современных ЭВМ сужает необходимость исчисления средних по упрощенным схемам.

2. Средняя гармоническая

2.2 Средняя гармоническая простая. Если объёмы явлений, т.е. произведения  Х_i ×f_i  по каждой единице равны, то для расчёта средней применяется формула средней гармонической простой:

 

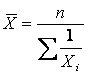
Например: Две автомашины прошли один и тот же путь: первая со скоростью 60 км/ч, вторая со скоростью 80 км/ч. Определить среднюю скорость движения автомашины.

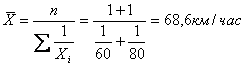
2.2 Средняя гармоническая взвешенная. Учитывая, что средние выражают качественные свойства изучаемых явлений, важно правильно выбрать вид средней  исходя из взаимосвязей явлений и признаков. Когда статистическая информация не содержит частот (f_i ) у отдельных вариант (X), а представлена как их произведение M_i=(X_i × f_i), то для расчёта средней применяется формула средней гармонической взвешенной:

 

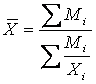
Например: По имеющимся данным о продаже хлеба «Дарницкий» определить среднюю цену одной булки хлеба

№ торгового павильона	Цена одной булки хлеба «Дарницкий» весом 0,5 кг, руб. (Xi)	Сумма выручки от продажи хлеба «Дарницкий», руб. (Mi)	Количество проданных булок , шт
1	10,40	10400	1000
2	9,60	4800	500
3	11,20	11200	1000
Итого:		26400	2500

Средняя цена одной булки хлеба может быть определена делением общей суммы выручки от продажи хлеба на общее количество проданных булок

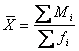 (1). Но количество проданных булок в каждом торговом павильоне неизвестно, его можно выразить, учитывая особенность исходных данных, делением суммы выручки от продажи хлеба на цену одной булки  (2). Подставим значение (f_i) – формулу (2) в формулу (1) и получим

 - формулу средней гармонической взвешенной

Средняя цена одной булки хлеба составляет:

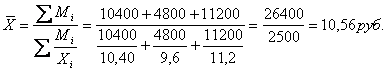
Используя для расчёта средней цены формулу средней арифметической простой, получим , что является неверным результатом, так как не учтено количество проданных булок.

Средняя гармоническая представляет собой обратную величину средней арифметической из обратных значений осредняемого признака. Если определить частоты ряда распределения, то можно использовать формулу средней арифметической взвешенной, но формула средней гармонической взвешенной позволяет избежать промежуточных расчётов.

3.Средняя геометрическая

3.1 Средняя геометрическая простая применяется для характеристики  средних темпов роста в рядах динамики с равноотстоящими уровнями и исчисляется по формуле:

где    Х_i - цепной коэффициент роста уровня ряда динамики.

n – число цепных коэффициентов роста в ряду динамики.

3.2 Средняя геометрическая взвешенная применяется для характеристики  средних темпов роста в рядах динамики с неравноотстоящими уровнями и исчисляется по формуле:

где f_i – промежуток времени между датами.

4. Средняя хронологическая

4.1 Средняя хронологическая простая

Средний уровень моментного ряда динамики с равноотстоящими уровнями характеризует средняя хронологическая простая, которая исчисляется по

формуле:

где    X_i – значение уровня моментного ряда динамики;

n – число уровней моментного ряда динамики.

Например: По имеющимся данным определить средний товарный запас за первое полугодие

Дата	1 января	1 февраля	1 марта	1 апреля	1 мая	1 июня	1 июля
Товарный запас на указанную дату, тыс. руб.	984	1020	1003	998	1260	1254	1190
обозначение	X1	X2	X3	X4	X5	X6	X7

п=7

Средний товарный запас за полугодие составляет

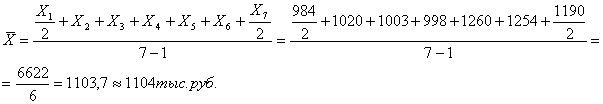
4.2 Средняя хронологическая взвешенная

Средний уровень моментного ряда динамики с неравноотстоящими уровнями характеризует средняя хронологическая взвешенная, которая исчисляется по формуле:

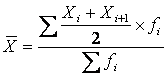
X_i  и X_i+1  – значение уровня моментного ряда динамики и уровня, следующего за ним;.  

где f_i – промежуток времени между датами.

Например: Известна списочная численность персонала организации на  некоторые даты 2009 года. Определить среднесписочную численность персонала за год.

Дата	1.01.2009	1.03.2009	1.06.2009	1.09.2009	1.01.2010
Численность персонала по списку на указанную дату, чел.	1200	1100	1250	1500	1350

Среднесписочная численность персонала за 2009 год составляет

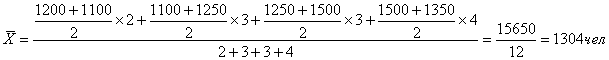
5. Средняя квадратическая

5.1 Средняя квадратическая простая применяется, когда возникает потребность расчета среднего размера признака, выраженного в квадратных единицах измерения, для несгруппированных данных. Она исчисляется как квадратный корнень из частного от деления суммы квадратов отдельных значений признака на их число по формуле:

.

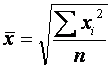где f_i – частота ряда распределения или удельный вес в совокупности.

5.2. Средняя квадратическая взвешенная применяется, когда возникает потребность расчета среднего размера признака, выраженного в квадратных единицах измерения, для сгруппированных данных. Исчисляется по формуле:

,

где f_i – частота ряда распределения или удельный вес в совокупности.

6. Средняя кубическая

6.1 Средняя кубическая простая применяется, когда возникает потребность расчета среднего размера признака, выраженного в кубических единицах измерения, для несгруппированных данных. Исчисляется по формуле:

 

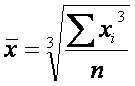
6.2 Средняя кубическая взвешенная применяется, когда возникает потребность расчета среднего размера признака, выраженного в кубических единицах измерения, для сгруппированных данных. Исчисляется по формуле:

.

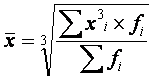Правило мажорантности средних величин

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.