ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.
Расчёт структурных характеристик
вариационного ряда распределения.
Студент
должен:
знать:
- область применения и методику расчёта структурных
средних величин;
уметь:
- исчислять структурные средние величины;
- формулировать вывод по полученным результатам.
Методические указания
В
статистике исчисляются мода и медиана, которые относятся к структурным средним,
так как их величина зависит от строения статистической совокупности.
Расчёт моды
Модой называется значение признака
(варианта), чаще всеговстречающееся в изучаемой
совокупности. В дискретном ряду распределения модой будет варианта с наибольшей
частотой.
Например: Распределение проданной женской обуви по размерам характеризуется
следующим образом:
|
Размер
обуви |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
|
Количество
проданных пар |
8 |
19 |
34 |
108 |
72 |
51 |
6 |
2 |
В этом ряду
распределения модой является 37 размер,
т.е. Мо=37 размер.
Для
интервального ряда распределения мода определяется по формуле:
![]()
где ХMo -
нижняя граница модального интервала;
hMo - величина модального интервала;
fMo –
частота модального интервала;
fMo-1 и
fMo+1 – частота интервала соответственно
предшествующего модальному и следующего за ним.
Например:
Распределение рабочих по стажу работы характеризуется следующими данными.
|
Стаж работы, лет |
до 2 |
2-4 |
4-6 |
6-8 |
8-10 |
10 и более |
|
Число рабочих, чел. |
4 |
23 |
20 |
35 |
11 |
7 |
Определить моду
интервального ряда распределения.
Мода интервального ряда составляет
![]()
Мода всегда бывает
несколько неопределённой, т.к. она зависит от величины групп и точного
положения границ групп. Мода широко применяется в коммерческой практике при
изучении покупательского спроса, при регистрации цен и т.п.
Расчёт медианы
Медианой в статистике называется варианта,
расположенная в середине упорядоченного ряда данных, и которая делит
статистическую совокупность на две равные части так, что у одной половины
значения меньше медианы, а у другой половины – больше её. Для определения
медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания
или убывания индивидуальных значений признака.
В дискретном
упорядоченном ряду с нечётным числом членов медианой будет варианта,
расположенная в центре ряда.
Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7
лет, т.е. Ме=7 лет
Если дискретный
упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя
арифметическая из двух смежных вариант, стоящих в центре ряда.
Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду
имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя
арифметическая из этих значений и будет медианой ряда
![]()
Чтобы определить медиану для
сгруппированных данных, необходимо считать накопленные частоты.
Например: По имеющимся данным определим медиану размера обуви
|
Размер обуви |
Количество проданных пар |
Сумма накопленных частот |
|
34 |
8 |
8 |
|
35 |
19 |
8+19=27 |
|
36 |
34 |
27+34=61 |
|
37 |
108 |
61+108=169 |
|
38 |
72 |
- |
|
39 |
51 |
- |
|
40 |
6 |
- |
|
41 |
2 |
- |
|
Итого |
300 |
|
Для
определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание
итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот
ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная
сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е.
37 и есть медиана ряда.
Если
же сумма накопленных частот против одной из вариант равна точно половине суммы
частот ряда, то медиана определяется как средняя арифметическая этой варианты и
последующей.
Например: По имеющимся данным определим медиану заработной платы рабочих
|
Месячная заработная плата, тыс.руб. |
Число рабочих, чел. |
Сумма накопленных частот |
|
14,0 |
2 |
2 |
|
14,2 |
6 |
2+6=8 |
|
16,0 |
12 |
8+12=20 |
|
16,8 |
16 |
- |
|
18,0 |
4 |
- |
|
Итого: |
40 |
- |
Медиана будет равна: ![]()
Медиана
интервального вариационного ряда распределения определяется по формуле:
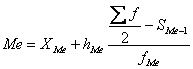
Где ХМе – нижняя граница медианного интервала;
hMe –
величина медианного интервала;
∑f
- сумма частот ряда;
fМе – частота медианного интервала;
Например: По имеющимся данным о распределении предприятий по численности
промышленно – производственного персонала рассчитать медиану в интервальном
вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
7 |
4+7=11 |
|
400-500 |
30 |
11+30=41 |
|
500-600 |
19 |
- |
|
600-700 |
15 |
- |
|
700-800 |
5 |
|
|
Итого: |
80 |
|
Определим, прежде всего,
медианный интервал. В данном примере сумма накопленных частот, превышающих половину
суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный
интервал, т.е. интервал, в котором находится медиана ряда. Определим её
значение
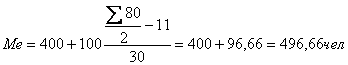
Если же сумма накопленных частот
против одного из интервалов равна точно половине суммы частот ряда, то медиана
определяется по формуле:
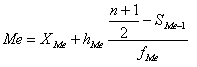
где n – число
единиц в совокупности.
Например: По имеющимся данным о распределении предприятий по
численности промышленно – производственного персонала рассчитать медиану в
интервальном вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
6 |
4+6=10 |
|
400-500 |
30 |
10+30=40 |
|
500-600 |
20 |
40+20=60 |
|
600-700 |
15 |
- |
|
700-800 |
5 |
|
|
Итого: |
80 |
|
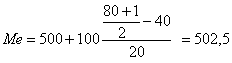 чел
чел
Моду и медиану в
интервальном ряду можно определить
графически:
моду
в дискретных рядах - по полигону распределения, моду в интервальных рядах - по
гистограмме распределения, а медиану - по кумуляте.
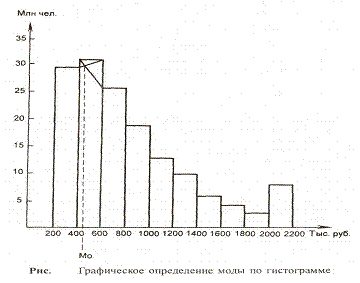
Мода интервального ряда распределения
определяется по гистограмме распределения определяют
следующим образом. Для этого выбирается самый высокий прямоугольник, который
является в данном случае модальным. Затем правую вершину модального
прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.
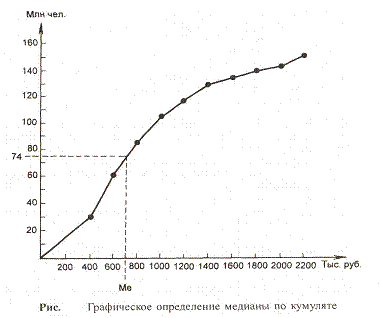
Медиана рассчитывается по
кумуляте. Для её определения из точки на шкале
накопленных частот (частостей), соответствующей 50%,
проводится прямая, параллельная оси абсцисс, до
пересечения с кумулятой. Затем из точки пересечения
указанной прямой с кумулятой опускается перпендикуляр
на ось абсцисс. Абсцисса точки пересечения является медианой.
Кроме моды и медианы в вариантных рядах могут быть
определены и другие структурные характеристики – квантили. Квантили
предназначены для более глубокого изучения структуры ряда распределения.
Квантиль – это значение
признака, занимающее определенное место в упорядоченной по данному признаку
совокупности. Различают следующие виды квантилей:
- квартили – значения признака, делящие упорядоченную
совокупность на четыре
равные части;
- децили
– значения признака, делящие упорядоченную совокупность на десять
равных частей;
- перцентели -
значения признака, делящие упорядоченную совокупность на сто равных частей.
Таким образом, для характеристики положения центра ряда распределения
можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя
центра распределения необходимо исходить из следующих рекомендаций:
-
для устойчивых социально-экономических
процессов в качестве показателя центра используют среднюю
арифметическую. Такие процессы характеризуются симметричными распределениями, в
которых ![]() ;
;
-
для неустойчивых процессов положение
центра распределения характеризуется с помощью Mo
или Me. Для асимметричных процессов предпочтительной
характеристикой центра распределения является медиана, поскольку занимает
положение между средней арифметической и модой.